Diferencia entre expresiones y ecuaciones algebraicas

Expresiones algebraicas vs ecuaciones
El álgebra es una de las principales ramas de las matemáticas y define algunas de las operaciones fundamentales que contribuyen a la comprensión humana de las matemáticas, como la adición, la resta, la multiplicación y la división. El álgebra también presenta el concepto de variables, que permite que una cantidad desconocida se represente con una sola letra, de ahí la conveniencia de la manipulación en las aplicaciones.
Más sobre expresiones algebraicas
Un concepto o una idea se puede expresar matemáticamente utilizando las herramientas básicas disponibles en el álgebra. Tal expresión se conoce como una expresión algebraica. Estas expresiones consisten en números, variables y diferentes operaciones algebraicas.
Por ejemplo, considere la declaración "Para formar la mezcla, agregue 5 tazas de x y 6 tazas de y". Es razonable expresar la mezcla como 5x+6y. No sabemos qué o cuánto son X e Y, pero da las medidas relativas en la mezcla. La expresión tiene sentido, pero no completo, sentido matemáticamente. x/y, x2+y, xy+xC son todos ejemplos de expresiones.
Para facilitar el uso, el álgebra presenta su propia terminología para las expresiones.
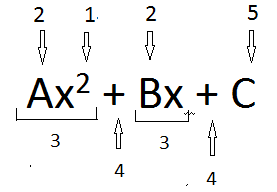
1. El exponente 2. Coeficientes 3. Término 4. Operador algebraico 5. Una constante
norte.B: Una constante también se puede usar como coeficiente.
Además, al realizar operaciones algebraicas (E.gramo. Al simplificar una expresión), la precedencia del operador debe seguirse. Precedencia del operador (prioridad) en orden descendente es la siguiente;
Soportes
De
División
Multiplicación
Suma
Sustracción
Este orden es comúnmente conocido por la mnemónica formada por las primeras letras de cada operación, que es Bodmas.
Históricamente, la expresión y operaciones algebraicas trajeron una revolución en las matemáticas porque la formulación de conceptos matemáticos fue más fácil, por lo que son las siguientes derivaciones o conclusiones. Antes de este formulario, los problemas se resolvieron principalmente usando relaciones.
Más sobre ecuación algebraica
Se forma una ecuación algebraica conectando dos expresiones utilizando un operador de asignación que denota la igualdad de los dos lados. Da que el lado izquierdo es igual al lado derecho. Por ejemplo, x2-2x+1 = 0 y x/y-4 = 3x2+Y son ecuaciones algebraicas.
Por lo general, las condiciones de igualdad se cumplen solo para ciertos valores de las variables. Estos valores se conocen como soluciones de la ecuación. Cuando se sustituye, estos valores agotan las expresiones.
Si una ecuación consiste en polinomios en ambos lados, la ecuación se conoce como ecuación polinomial. Además, si solo una variable está en la ecuación, se conoce como una ecuación univariada. Para dos o más variables, la ecuación se llama ecuaciones multivariadas.
¿Cuál es la diferencia entre expresiones y ecuaciones algebraicas??
• La expresión algebraica es una combinación de variables, constantes y operadores, de modo que forman un término o más para dar un sentido parcial de relaciones entre cada variable. Pero las variables pueden asumir cualquier valor disponible en su dominio.
• Una ecuación es dos o más expresiones con una condición de igualdad y la ecuación es verdadera para uno o varios valores de las variables. Una ecuación tiene mucho sentido siempre que no se viole la condición de igualdad.
• Una expresión se puede evaluar para valores dados.
• Se puede resolver una ecuación para encontrar una cantidad o variable desconocida, debido al hecho anterior. Los valores se conocen como la solución a la ecuación.
• La ecuación lleva un signo igual (=) en la ecuación.