Diferencia entre la distribución binomial y normal

Binomial vs Distribución normal
 

Las distribuciones de probabilidad de las variables aleatorias juegan un papel importante en el campo de las estadísticas. De esas distribuciones de probabilidad, la distribución binomial y la distribución normal son dos de las más comunes en la vida real.

¿Qué es la distribución binomial??

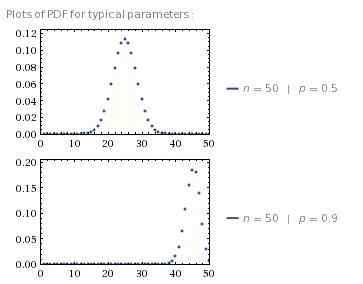
La distribución binomial es la distribución de probabilidad correspondiente a la variable aleatoria X, cuál es el número de éxitos de un secuencia finita de experimentos independientes de sí/no, cada uno de los cuales tiene una probabilidad de éxito pag. De la definición de X, Es evidente que es una variable aleatoria discreta; Por lo tanto, la distribución binomial también es discreta.

La distribución se denota como X ~B(norte,pag) dónde norte es el número de experimentos y p es la probabilidad de éxito. Según la teoría de la probabilidad, podemos deducir que B(norte,pag) sigue la función de masa de probabilidad [látex] b (n, p) \\ sim \\ binom n k p^k (1-p)^(n-k), k = 0, 1, 2, ... n [/látex]. De esta ecuación, se puede deducir aún más que el valor esperado de X, MI(X) = notario público y la varianza de X, V (X) = notario público(1-pag).

Por ejemplo, considere un experimento aleatorio de lanzar una moneda 3 veces. Definir el éxito como obteniendo H, falla como obteniendo t y la variable aleatoria X como el número de éxitos en el experimento. Entonces X~B(3, 0.5) y la función de masa de probabilidad de X Dado por [látex] \\ binom 3 k 0.5^k (0.5)^(3-k), k = 0, 1, 2.[/látex]. Por lo tanto, la probabilidad de obtener al menos 2 h es P (X ≥ 2) = P (X = 2 o X = 3) = P (X = 2) + P (X = 3) = ³C₂(0.5²) (0.5¹) + ³C₃(0.5³) (0.5⁰) = 0.375 + 0.125 = 0.5.

¿Qué es la distribución normal??

La distribución normal es la distribución de probabilidad continua definida por la función de densidad de probabilidad, [látex] n (\\ mu, \\ sigma) \\ sim \\ frac 1 \\ sqrt 2 \\ pi \\ sigma^ 2 \\ e^- \\ frac (x- \\ mu)^2 2 \\ sigma^2 [/latex]. Los parámetros [látex] \\ mu y \\ sigma [/látex] denotan la media y la desviación estándar de la población de interés. Cuando [látex] \\ mu = 0 y \\ sigma = 1 [/látex] la distribución se llama distribución normal estándar.

Esta distribución se llama normal ya que la mayoría de los fenómenos naturales siguen la distribución normal. Porque, por ejemplo, el coeficiente intelectual de la población humana se distribuye normalmente. Como se ve en el gráfico, es unimodal, simétrico sobre la media y la campana en forma de. La media, el modo y la mediana coinciden. El área debajo de la curva corresponde a la parte de la población, satisfaciendo una condición dada.

Las porciones de población en el intervalo [látex] (\\ mu - \\ sigma, \\ mu + \\ sigma) [/látex], [látex] (\\ mu - 2 \\ sigma, \\ mu + 2 \\ Sigma) [/latex], [látex] (\\ mu - 3 \\ Sigma, \\ Mu + 3 \\ Sigma) [/látex] son ​​aproximadamente 68.2%, 95.6% y 99.8% respectivamente.

¿Cuál es la diferencia entre distribuciones binomiales y normales??

• La distribución binomial es una distribución de probabilidad discreta, mientras que la distribución normal es continua.
• La función de masa de probabilidad de la distribución binomial es [látex] b (n, p) \\ sim \\ binom n k p^k (1-p)^(n-k) [/latex] , mientras que la función de densidad de probabilidad de la distribución normal es [látex] n (\\ mu, \\ sigma) \\ sim \\ frac 1 \\ sqrt 2 \\ pi \\ sigma^2 \\ e^- \\ frac (x- \\ mu)^2 2 \\ sigma^2 [/latex]
• La distribución binomial se aproxima con la distribución normal bajo ciertas condiciones, pero no al revés.