Diferencia entre coordenadas cartesianas y coordenadas polares

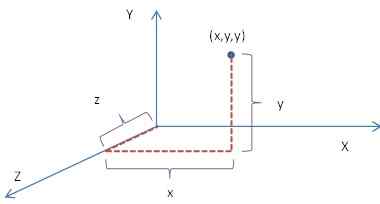
Coordenadas cartesianas vs coordenadas polares
 

En la geometría, un sistema de coordenadas es un sistema de referencia, donde los números (o coordenadas) se utilizan para determinar de manera única la posición de un punto u otro elemento geométrico en el espacio. Los sistemas de coordenadas permiten que los problemas geométricos se conviertan en un problema numérico, que proporciona la base para la geometría analítica.

El sistema de coordenadas cartesianas y los sistemas de coordenadas polares son dos de los sistemas de coordenadas comunes utilizados en matemáticas.

Coordenadas cartesianas

El sistema de coordenadas cartesianas utiliza la línea de números reales como referencia. En una dimensión, la línea numérica se extiende desde el infinito negativo hasta el infinito positivo. Teniendo en cuenta el punto 0 como inicio, la longitud a cada punto se puede medir. Esto proporciona una forma única de identificar una posición en la línea, con un solo número.

El concepto se puede extender a dos y tres dimensiones donde se utilizan líneas numéricas perpendiculares entre sí. Todos comparten el mismo punto 0 que el comienzo. Las líneas numéricas se denominan ejes, y a menudo se llaman eje x, eje y eje z. La distancia a un punto a lo largo de cada eje a partir de (0, 0, 0), que también se conoce como el origen, y se da como una tupla se conoce como la coordenada del punto. Un punto general en este espacio puede ser representado por la coordenada (x, y, z). En un sistema plano donde solo hay dos ejes, las coordenadas se dan como (x, y). Un plano creado por los ejes se conoce como plano cartesiano, y a menudo se hace referencia por las letras de los ejes. mi.gramo. Avión xy.

Este punto general puede usarse para describir diferentes elementos geométricos al restringir el punto general para comportarse de manera específica. Por ejemplo, la ecuación x^2+y^2 = a^2 representa un círculo. En lugar de dibujar un círculo con radio A, es posible denotar el círculo con una forma más abstracta que se muestra arriba.

Coordenadas polares

Las coordenadas polares usan un sistema de referencia de diferencia para denotar un punto. El sistema de coordenadas polares utiliza el ángulo de antihorario de la dirección positiva del eje x y la distancia de línea recta hasta el punto a medida que las coordinan. 

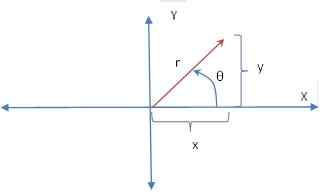
Las coordenadas polares se pueden representar como anteriormente en el sistema de coordenadas cartesianas bidimensionales.

La transformación entre los sistemas polares y cartesianos viene dada por las siguientes relaciones:

r = √ (x² + Y²) ↔ x = r cosθ, y = r sinθ

θ = bronceado^-1 (x/y)

¿Cuál es la diferencia entre las coordenadas cartesianas y polares??

• Las coordenadas cartesianas usan líneas numéricas como ejes, y se puede usar en una, dos o tres dimensiones. Por lo tanto, tiene la capacidad de representar geometrías lineales, planas y sólidas.

• Las coordenadas polares usan un ángulo y una longitud como coordenadas, y puede representar solo geometrías lineales y planas, aunque puede desarrollarse en un sistema de coordenadas cilíndricas, para representar geometrías sólidas.

• Ambos sistemas se utilizan para representar números imaginarios definiendo el eje imaginario y desempeñan un papel vital en el álgebra compleja. Aunque, en forma simple, las coordenadas cartesianas son números reales (x, y, z) Las coordenadas en el sistema polar no siempre son números reales; i.mi.  Si el ángulo se da en los grados, las coordenadas no son reales; Si el ángulo se da en las coordenadas de radianes son números reales.