Diferencia entre el circumcenter, el incentrador, el ortocentro y el centroide
Circumenter, Incenter, ortocentro vs centroide
Circumenter: El circumenter es el punto de intersección de tres bisectores perpendiculares de un triángulo. Ciruscenter es el centro de la circunscribir, que es un círculo que pasa a través de los tres vértices de un triángulo.
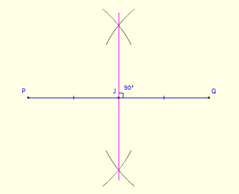
Para dibujar el circumentro, cree dos bisectores perpendiculares a los lados del triángulo. El punto de intersección da al circumentro. Se puede crear un bisector utilizando la brújula y el borde recto de la regla. Establezca la brújula en un radio, que es más de la mitad de la longitud del segmento de línea. Luego haga dos arcos a cada lado del segmento con un extremo como el centro del arco. Repita el proceso con el otro extremo del segmento. Los cuatro arcos crean dos puntos de intersección a cada lado del segmento. Dibuja una línea que une estos dos puntos con la ayuda de la regla, y eso dará al bisector perpendicular del segmento.
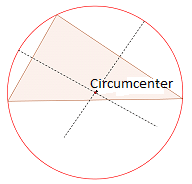
Para crear el circumircle, dibuje un círculo con el circunstancia como el centro y la longitud entre el circumcenter y un vértice como el radio del círculo.
En el centro: El incentrador es el punto de intersección de los tres bisectrizs. El incentrador es el centro del círculo con el circunferencia intersectando los tres lados del triángulo.
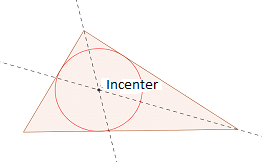
Para dibujar el incentivo de un triángulo, cree dos internos Bisectores de ángulo del triángulo. El punto de intersección de los dos bisectores de ángulo le da al incentivo. Para dibujar el bisector de ángulo, haga dos arcos en cada uno de los brazos con el mismo radio. Esto proporciona dos puntos (uno en cada brazo) en los brazos del ángulo. Luego tomando cada punto en los brazos como los centros, dibuje dos arcos más. El punto construido por la intersección de estos dos arcos da un tercer punto. Una línea que une el vértice del ángulo y el tercer punto le da al ángulo bisector.
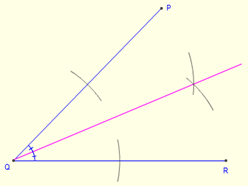
Para crear el incircar, Construya un segmento de línea perpendicular a cualquier lado, que está pasando por el incentivo. Tomando la longitud entre la base de la perpendicular y el incentor como radio, dibuja un círculo completo.
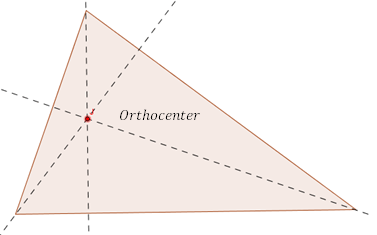
Ortocentro: El ortocentro es el punto de intersección de las tres alturas (altitudes) del triángulo.

Para crear el ortocentro, dibuja dos Altitudes de un triángulo. Un segmento de línea perpendicular a un lado que pasa a través del vértice opuesto se llama altura. Para dibujar una línea perpendicular que pasa a través de un punto, primero marque dos arcos en la línea con el punto como el centro. Luego, cree otros dos arcos con cada uno de los puntos de intersección como el centro. Dibuje un segmento de línea que une el primer punto y el punto finalmente construido, y eso da la línea perpendicular al segmento de línea y pasa por el primer punto. El punto de intersección de las dos alturas le da al ortocentro.
Centroide: El centroide es el punto de intersección de los tres medianas de un triángulo. El centroide divide cada mediana en la relación 1: 2, y el centro de masa de una lámina triangular uniforme se encuentra en este punto.
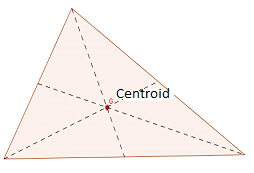
Para determinar el centroide, cree dos medianas del triángulo. Para crear una mediana, marque el punto medio de un lado. Luego construya un segmento de línea que une el punto medio y el vértice opuesto del triángulo. El punto de intersección de las medianas da al centroide de un triángulo.
¿Cuáles son las diferencias entre el circumceder, el incentor, el ortocentro y el centroide?
• Cirumcenter se crea utilizando los bisectores perpendiculares del triángulo.
• Los incentros se crean usando los ángulos bisectores de los triángulos.
• El ortocentro se crea utilizando las alturas (altitudes) del triángulo.
• El centroide se crea usando las medianas del triángulo.
• Tanto el Cirumcenter como el Incenter tienen círculos asociados con propiedades geométricas específicas.
• Centroide es el centro geométrico del triángulo, y es el centro de masa de un laminar triangular uniforme.
• Para un triángulo no equilibrado, el Cirumcente, el ortocentro y el centroide se encuentran en línea recta, y la línea se conoce como la Línea de Euler.


