Diferencia entre el punto fijo y el punto de equilibrio
El diferencia clave entre el punto fijo y el punto de equilibrio es que El punto fijo es útil para encontrar el estado estable de un sistema, mientras que el punto de equilibrio es el estado en el que el sistema no cambia a medida que las variables del sistema cambiand.
El punto fijo y el punto de equilibrio son términos útiles en matemáticas para identificar el estado estable de un sistema físico deseado.
CONTENIDO
1. Descripción general y diferencia de claves
2. ¿Qué es el punto fijo?
3. ¿Qué es el punto de equilibrio?
4. Similitudes entre el punto fijo y el punto de equilibrio
5. Comparación de lado a lado: punto fijo vs punto de equilibrio en forma tabular
6. Resumen
¿Qué es el punto fijo??
El punto fijo de una función en matemáticas es un elemento del dominio de esa función que se puede asignar a sí misma a través de la función. En otras palabras, "C" es un punto fijo de la función "F" cuando f (c) = c. Esto también se conoce como fixpoint o punto invariante. Por lo tanto, f (f (... f (c) ...)) = Fnorte(c) = c que es una preocupación importante de terminación con respecto a la calculación recursiva "F". Podemos nombrar un conjunto de puntos fijos como un conjunto fijo.
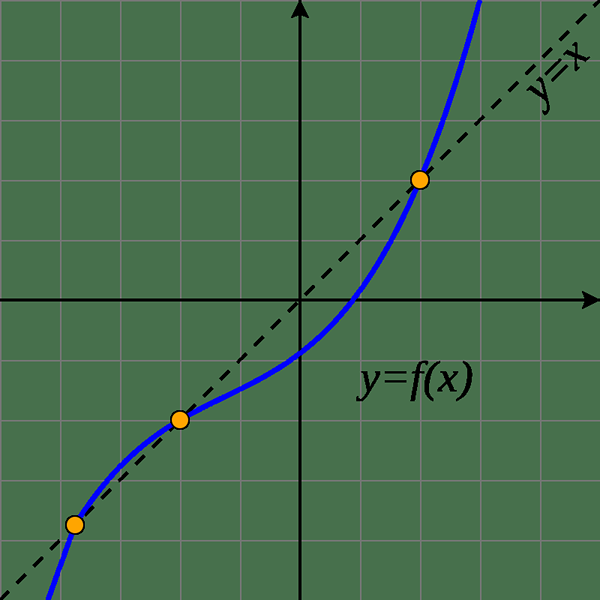
Consideremos un ejemplo para comprender este fenómeno. Si tomamos "f" en números reales por f (x) = x2 - 3x +4, entonces 2 es un punto fijo de "F" porque F (2) = 2. Sin embargo, todas las funciones no tienen puntos fijos. mi.gramo. Cuando f (x) = x + 1, no tiene puntos fijos porque "x" nunca equivale a "x +1" para ningún número real. Teniendo en cuenta la terminología gráfica, un punto fijo "x" se refiere al punto (x, f (x)) que está en la línea y = x. En otras palabras, el gráfico de "F" contiene un punto en común con esa línea.

Los puntos fijos son puntos periódicos que tienen su período igual a uno. Teniendo en cuenta la geometría proyectiva, los puntos fijos de una proyectividad se nombran como puntos dobles. Según la teoría de Galois, la serie de puntos fijos de un conjunto de automorfismos de campo se nombra como un campo fijo de ese conjunto de automorfismos.
Existen diferentes aplicaciones de puntos fijos, que incluyen economía, física, compiladores de lenguaje de programación, teoría de tipos, el vector en los valores de PageRank de todas las páginas web, la distribución estacionaria de la cadena Markov, etc.
¿Qué es el punto de equilibrio??
Un punto de equilibrio es una solución constante para una ecuación diferente en matemáticas. Este término viene principalmente bajo ecuaciones diferenciales en matemáticas. Podemos clasificar los equilibrios observando los signos de los valores propios de la linealización de las ecuaciones sobre los equilibrios. En otras palabras, podemos clasificar los equilibrios evaluando la matriz jacobiana en los puntos de equilibrio del sistema deseado, seguido de encontrar los valores propios resultantes. Allí, podemos determinar el comportamiento del sistema en el vecindario de los puntos de equilibrio cuantitativamente al encontrar los vectores propios que están asociados con los valores propios.
Podemos decir que un punto de equilibrio es hiperbólico cuando ninguno de los valores propios tiene cero parte real. Sin embargo, si todos los valores propios tienen una parte real negativa, entonces el equilibrio se convierte en una ecuación estable. Del mismo modo, si hay una parte real positiva, entonces el equilibrio se vuelve inestable. Además, si hay al menos una parte real negativa y al menos una parte real positiva en los valores propios, entonces el equilibrio obtiene un punto de silla.
¿Cuáles son las similitudes entre el punto fijo y el punto de equilibrio??
- Estos puntos pueden no ser estables.
- Ambos puntos se describen para una condición de estado estacionario de un sistema.
¿Cuál es la diferencia entre el punto fijo y el punto de equilibrio??
El punto fijo y el punto de equilibrio se utilizan en matemáticas. La diferencia clave entre el punto fijo y el punto de equilibrio es que el punto fijo es útil para encontrar el estado estable de un sistema, mientras que el punto de equilibrio es el estado en el que el sistema no cambia a medida que las variables del sistema se cambian.

Resumen -punto fijo vs punto de equilibrio
El punto fijo y el punto de equilibrio son términos útiles en matemáticas para identificar el estado estable de un sistema físico deseado. La diferencia clave entre el punto fijo y el punto de equilibrio es que el punto fijo es útil para encontrar el estado estable de un sistema, mientras que el punto de equilibrio es el estado en el que el sistema no cambia a medida que las variables del sistema se cambian.
Referencia:
1. "Punto fijo (matemáticas)." Wikipedia, Fundación Wikimedia, 26 mar. 2021, disponible aquí.
Imagen de cortesía:
1. "Ejemplo de punto fijo" de Krishnavedala - Trabajo propio (CC0) a través de Commons Wikimedia


