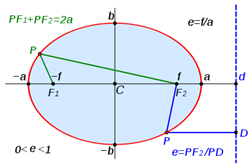
Diferencia entre hipérbola y elipse
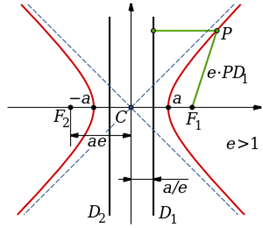
Hyperbola vs elipse
Cuando un cono se corta en diferentes ángulos, se marcan diferentes curvas por el borde del cono. Estas curvas a menudo se llaman secciones cónicas. Más precisamente, una sección cónica es una curva obtenida al intersectar una superficie cónica circular derecha con una superficie plana. En diferentes ángulos de intersección, se dan diferentes secciones cónicas.
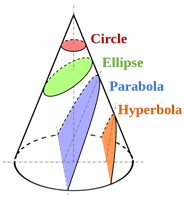
Tanto la hipérbola como las elipse son secciones cónicas, y sus diferencias se comparan fácilmente en este contexto.
Más sobre elipse
Cuando la intersección de la superficie cónica y la superficie del plano produce una curva cerrada, se conoce como elipse. Tiene una excentricidad entre cero y uno (0 El segmento de línea que pasa a través de los focos se conoce como el eje principal, y el eje perpendicular al eje principal y que pasa por el centro de la elipse se conoce como el eje menor. Los diámetros a lo largo de cada eje se conocen como diámetro transversal y el diámetro del conjugado respectivamente. La mitad del eje principal se conoce como el eje semi-mayor, y la mitad del eje menor se conoce como el eje semi-minor. Cada punto F1 y F2 se conocen como los focos de la elipse y las longitudes F1 + PF2 = 2a , dónde PAG es un punto arbitrario en la elipse. Excentricidad mi se define como la relación entre la distancia desde un enfoque hasta el punto arbitrario ( PF2 ) y la distancia perpendicular al punto arbitrario desde la directriz (Pd). También es igual a la distancia entre los dos focos y el eje semi-mayor: mi = PF/PD = fa La ecuación general de la elipse, cuando el eje semi-mayor y el eje semi-minor coinciden con los ejes cartesianos, se proporciona de la siguiente manera. X2/a2 + Y2/b2 = 1 La geometría de la elipse tiene muchas aplicaciones, especialmente en física. Las órbitas de los planetas en el sistema solar son elípticos con el sol como un enfoque. Los reflectores para antenas y dispositivos acústicos se hacen en forma elíptica para aprovechar el hecho de que cualquier forma de emisión un enfoque convergerá en el otro enfoque. Más sobre Hyperbola La hipérbola también es una sección cónica, pero está abierta. El término hipérbola se refiere a las dos curvas desconectadas que se muestran en la figura. En lugar de cerrar como una elipse de los brazos o las ramas de la hipérbola continúan hasta el infinito. Los puntos donde las dos ramas tienen la distancia más corta entre ellas se conocen como vértices. La línea que pasa a través de los vértices se considera el eje principal o el eje transversal, y es uno de los ejes principales de la hipérbola. Los dos focos de la parábola también se encuentran en el eje principal. El punto medio de la línea entre los dos vértices es el centro, y la longitud del segmento de la línea es el eje semi-mayor. El bisector perpendicular del eje semi-mayor es el otro eje principal, y las dos curvas de la hipérbola son simétricas alrededor de este eje. La excentricidad de la parábola es mayor que una; E> 1. Si los ejes principales coinciden con los ejes cartesianos, la ecuación general de la hipérbola es de la forma: X2/a2 - Y2/b2 = 1, dónde a es el eje semi-mayor y b es la distancia desde el centro para enfocar. Las hipérbolas con extremos abiertos frente al eje X se conocen como Hyperbolas este-oeste. Hyperbolas similares también se pueden obtener en el eje Y. Estos se conocen como las hipérbolas del eje y. La ecuación para tales hipérbolas toma la forma Y2/a2 - X2/b2 = 1 ¿Cuál es la diferencia entre Hyperbola y Ellipse?? • Tanto las elipses como la hipérbola son secciones cónicas, pero la elipse es una curva cerrada, mientras que la hipérbola consta de dos curvas abiertas. • Por lo tanto, la elipse tiene perímetro finito, pero la hipérbola tiene una longitud infinita. • Ambos son simétricos alrededor de su eje mayor y menor, pero la posición de la directriz es diferente en cada caso. En la elipse, está fuera del eje semi-mayor mientras, en Hyperbola, se encuentra en el eje semi-mayor. • Las excentricidades de las dos secciones cónicas son diferentes. 0 miHipérbola > 0 • La ecuación general de las dos curvas se ve igual, pero son diferentes. • El bisector perpendicular del eje mayor se cruza con la curva en la elipse, pero no en la hipérbola. (Fuente de imágenes: Wikipedia)