Diferencia entre integración y suma

Integración vs suma
 

En las matemáticas de la escuela secundaria, la integración y la suma a menudo se encuentran en las operaciones matemáticas. Aparentemente se usan como herramientas diferentes y en diferentes situaciones, pero comparten una relación muy cercana.

Más sobre la suma

La suma es el funcionamiento de agregar una secuencia de números y la operación a menudo se denota por la letra griega de capital Sigma σ. Se utiliza para abreviar la suma y igual a la suma/total de la secuencia. A menudo se usan para representar la serie, que esencialmente son secuencias infinitas resumidas. También se pueden usar para indicar la suma de vectores, matrices o polinomios.

La suma generalmente se realiza para un rango de valores que pueden representarse por un término general, como una serie que tiene un término común. El punto de partida y el punto final de la suma se conocen como el límite inferior y el límite superior de la suma, respectivamente.

Por ejemplo, la suma de la secuencia a₁, a₂, a₃, a₄, … , a_norte es un₁ + a₂ + a₃ +… + A_norte que se puede representar fácilmente utilizando la notación de suma como ∑^norte_{i = 1} a_i; Me llaman el índice de suma.

Se utilizan muchas variaciones para la suma basada en la aplicación. En algunos casos, el límite superior y el límite inferior se pueden administrar como un intervalo o un rango, como ∑_1≤i≤100 a_i y ∑_{i∈ [1,100]} a_i. O se puede dar como un conjunto de números como ∑_i∈P a_i , donde p es un conjunto definido.

En algunos casos, se pueden usar dos o más signos de Sigma, pero se pueden generalizar de la siguiente manera; ∑_j ∑_k a_jk = ∑_{J, K} a_jk.

Además, la suma sigue muchas reglas algebraicas. Dado que la operación integrada es la adición, muchas de las reglas comunes del álgebra se pueden aplicar a las sumas en sí y para los términos individuales representados por la suma.

Más sobre la integración

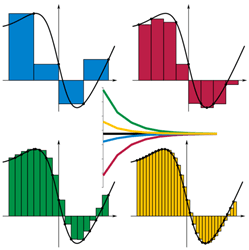
La integración se define como el proceso inverso de diferenciación. Pero en su vista geométrica también se puede considerar como el área encerrada por la curva de la función y el eje. Por lo tanto, el cálculo del área proporciona el valor de una integral definida como se muestra en el diagrama.

Fuente de la imagen: http: // en.Wikipedia.org/wiki/archivo: riemann_sum_convergence.png

El valor de la integral definitiva es en realidad la suma de las pequeñas tiras dentro de la curva y el eje. El área de cada tira es la altura × ancho en el punto del eje considerado. El ancho es un valor que podemos elegir, digamos ∆x. Y la altura es aproximadamente el valor de la función en el punto considerado, digamos F(X_i). Desde el diagrama, es evidente que cuanto más pequeñas son las tiras mejores, las tiras se ajustan dentro del área limitada, por lo tanto, una mejor aproximación del valor.

Entonces, en general la integral definitiva I, entre los puntos A y B (yo.e en el intervalo [a, b] donde unI ≅ F(X₁) ∆x + F(X₂) ∆x + ⋯ + F(X_norte) ∆x, donde n es el número de tiras (n = (b-a)/∆x). Esta suma del área se puede representar fácilmente utilizando la notación de suma como I ≅ ∑^norte_{i = 1} F(X_i) ∆x. Dado que la aproximación es mejor cuando ∆x es más pequeño, podemos calcular el valor cuando ∆x → 0. Por lo tanto, es razonable decir I = LIM_{∆x → 0} ∑^norte_{i = 1} F(X_i) ∆x.

Como generalización del concepto anterior, podemos elegir el ∆x basado en el intervalo considerado indexado por I (eligiendo el ancho del área en función de la posición). Entonces tenemos

I= LIM_{∆x → 0} ∑^norte_{i = 1} F(X_i) ∆x_i = _a∫^b F(x) dx

Esto se conoce como la integral Reimann de la función F(x) En el intervalo [A, B]. En este caso, A y B se conocen como el límite superior y el límite inferior de la integral. Reimann Integral es una forma básica de todos los métodos de integración.

En esencia, la integración es la suma del área cuando el ancho del rectángulo es infinitesimal.

¿Cuál es la diferencia entre la integración y la suma??

• La suma se suma una secuencia de números. Por lo general, la suma se da en esta forma ∑^norte_{i = 1} a_i Cuando los términos en la secuencia tienen un patrón y se pueden expresar utilizando un término general.

• La integración es básicamente el área limitada por la curva de la función, el eje y los límites superiores e inferiores. Esta área se puede administrar como la suma de áreas mucho más pequeñas incluidas en el área limitada.

• La suma implica los valores discretos con los límites superiores e inferiores, mientras que la integración implica valores continuos.

• La integración puede interpretarse como una forma especial de suma.

• En los métodos de cálculo numérico, la integración siempre se realiza como un resumen.