Diferencia entre las transformaciones de Laplace y Fourier

Transformaciones de Laplace vs Fourier
 

Tanto la transformación de Laplace como la transformación de Fourier son transformaciones integrales, que se emplean más comúnmente como métodos matemáticos para resolver sistemas físicos modelados matemáticamente. El proceso es simple. Un modelo matemático complejo se convierte en un modelo más simple y solucionable utilizando una transformación integral. Una vez que se resuelve el modelo más simple, se aplica la transformación integral inversa, lo que proporcionaría la solución al modelo original.

Por ejemplo, dado que la mayoría de los sistemas físicos dan como resultado ecuaciones diferenciales, se pueden convertir en ecuaciones algebraicas o en ecuaciones diferenciales fácilmente solucionables utilizando una transformación integral. Entonces resolver el problema será más fácil.

¿Cuál es la transformación de Laplace??

Dada una función F (T) de una variable real T, Su transformación de Laplace se define por la integral [látex] f (s) = \\ int_ 0^\\ infty e^-st f (t) dt [/latex] (siempre que existe), que es una función de una variable compleja s. Por lo general, se denota por L F (T). La transformación de laplace inversa de una función F(s) se toma como la función F (T) de tal manera que l F (T) = F(s), y en la notación matemática habitual que escribimos, l ^-1F(s) = F (T).La transformación inversa se puede hacer única si no se permiten funciones nulas. Uno puede identificar estos dos como operadores lineales definidos en el espacio de funciones, y también es fácil ver que, l ^-1L F (T) = F (T), si no se permiten funciones nulas.

La siguiente tabla enumera las transformaciones de laplace de algunas de las funciones más comunes.

¿Cuál es la transformación de Fourier??

Dada una función F (T) de una variable real T, Su transformación de Laplace se define mediante la integral [látex] f (\\ alpha) = \\ frac 1 \\ sqrt 2 \\ pi \\ int _ - \\ infty^\\ infty e^i \\ alpha t f (t) dt [/latex] (siempre que existe), y generalmente se denota por F F (T). La transformación inversa F ^-1F(α) viene dado por la integral [latex] f (t) = \\ frac 1 \\ sqrt 2 \\ pi \\ int _ - \\ infty^\\ infty e^ -i \\ alpha t f (\\ alpha) d \\ alfa [/látex]. La transformación de Fourier también es lineal y puede considerarse como un operador definido en el espacio de la función.

Usando la transformación de Fourier, la función original se puede escribir de la siguiente manera, siempre que la función tenga un número finito de discontinuidades y sea absolutamente integrable.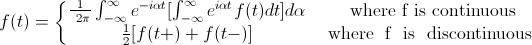

¿Cuál es la diferencia entre las transformaciones de Laplace y Fourier??

• Transformación de Fourier de una función F (T) se define como [latex] f (\\ alpha) = \\ frac 1 \\ sqrt 2 \\ pi \\ int _ - \\ infty^\\ infty e^i \\ alpha t f (t) dt [/latex], mientras que la transformación de laplace se define como [latex] f (s) = \\ int_ 0^\\ infty e^-st f (t) dt [/latex].
• La transformación de Fourier se define solo para las funciones definidas para todos los números reales, mientras que la transformación de Laplace no requiere que la función se define en los números reales negativos.
• Fourier Transform es un caso especial de la transformación de Laplace. Se puede ver que ambos coinciden para números reales no negativos. (i.mi. llevar s en el laplace para ser Iα + β dónde α y β son reales tal que mi ^β= ¹/_{√ (2ᴫ)})
• Cada función que tenga una transformación de Fourier tendrá una transformación de Laplace pero no viceversa.