Diferencia entre ecuaciones diferenciales lineales y no lineales

Ecuaciones diferenciales lineales vs no lineales
Una ecuación que contiene al menos un coeficiente diferencial o derivado de una variable desconocida se conoce como ecuación diferencial. Una ecuación diferencial puede ser lineal o no lineal. El alcance de este artículo es explicar qué es la ecuación diferencial lineal, qué es la ecuación diferencial no lineal y cuál es la diferencia entre las ecuaciones diferenciales lineales y no lineales.
Desde el desarrollo del cálculo en el siglo XVIII por los matemáticos como Newton y Leibnitz, la ecuación diferencial ha jugado un papel importante en la historia de las matemáticas. Las ecuaciones diferenciales son de gran importancia en las matemáticas debido a su gama de aplicaciones. Las ecuaciones diferenciales están en el corazón de cada modelo que desarrollamos para explicar cualquier escenario o evento en el mundo, ya sea en física, ingeniería, química, estadísticas, análisis financiero o biología (la lista es infinita). De hecho, hasta que el cálculo se convirtió en una teoría establecida, las herramientas matemáticas adecuadas no estaban disponibles para analizar los problemas interesantes en la naturaleza.
Las ecuaciones resultantes de una aplicación específica de cálculo pueden ser muy complejas y, a veces, no solucionables. Sin embargo, hay otros que podemos resolver, pero pueden parecer parecidos y confusos. Por lo tanto, para una identificación más fácil, las ecuaciones diferenciales se clasifican por su comportamiento matemático. Lineal y no lineal es una de esas categorización. Es importante identificar la diferencia entre ecuaciones diferenciales lineales y no lineales.
¿Qué es una ecuación diferencial lineal??
Suponer que F: X → Y y f (x) = y, un Ecuación diferencial sin términos no lineales de la función desconocida Y y sus derivados se conocen como una ecuación diferencial lineal.
Impone la condición de que y no pueda tener términos de índice más altos como y2, Y3,... y múltiplos de derivados como
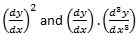
Tampoco puede contener términos no lineales como el pecado Y, miY^-2, o LN Y. Toma el formulario,
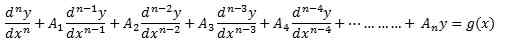
dónde Y y gramo son funciones de X. La ecuación es una ecuación diferencial de orden norte, cuál es el índice de la derivada de más alto orden.
En una ecuación diferencial lineal, el operador diferencial es un operador lineal y las soluciones forman un espacio vectorial. Como resultado de la naturaleza lineal del conjunto de soluciones, una combinación lineal de las soluciones también es una solución a la ecuación diferencial. Es decir, si Y1 y Y2 son soluciones de la ecuación diferencial, entonces C1 Y1+ C2 Y2 es también una solución.
La linealidad de la ecuación es solo un parámetro de la clasificación, y se puede clasificar en ecuaciones diferenciales homogéneas o no homogéneas y ordinarias o parciales. Si la función es gramo= 0 entonces la ecuación es una ecuación diferencial homogénea lineal. Si F es una función de dos o más variables independientes (F: X, T → Y) y f (x, t) = y , entonces la ecuación es una ecuación diferencial parcial lineal.
El método de solución para la ecuación diferencial depende del tipo y los coeficientes de la ecuación diferencial. El caso más fácil surge cuando los coeficientes son constantes. El ejemplo clásico para este caso es la segunda ley de movimiento de Newton y sus diversas aplicaciones. La segunda ley de Newton produce una ecuación diferencial lineal de segundo orden con coeficientes constantes.
¿Qué es una ecuación diferencial no lineal??
Las ecuaciones que contienen términos no lineales se conocen como ecuaciones diferenciales no lineales.
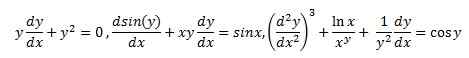
Todos arriba son ecuaciones diferenciales no lineales. Las ecuaciones diferenciales no lineales son difíciles de resolver, por lo tanto, se requiere un estudio cercano para obtener una solución correcta. En caso de ecuaciones diferenciales parciales, la mayoría de las ecuaciones no tienen una solución general. Por lo tanto, cada ecuación debe tratarse de forma independiente.
La ecuación de Navier-Stokes y la ecuación de Euler en la dinámica de fluidos, las ecuaciones de campo de la relatividad general de Einstein son ecuaciones diferenciales parciales no lineales bien conocidas. A veces, la aplicación de la ecuación de Lagrange a un sistema variable puede dar lugar a un sistema de ecuaciones diferenciales parciales no lineales.
¿Cuál es la diferencia entre ecuaciones diferenciales lineales y no lineales??
• Una ecuación diferencial, que tiene solo los términos lineales de la variable desconocida o dependiente y sus derivados, se conoce como ecuación diferencial lineal. No tiene término con la variable dependiente de índice superior a 1 y no contiene ningún múltiplo de sus derivadas. No puede tener funciones no lineales como funciones trigonométricas, función exponencial y funciones logarítmicas con respecto a la variable dependiente. Cualquier ecuación diferencial que contenga los términos mencionados anteriormente es una ecuación diferencial no lineal.
• Las soluciones de ecuaciones diferenciales lineales crean espacio vectorial y el operador diferencial también es un operador lineal en el espacio vectorial.
• Las soluciones de ecuaciones diferenciales lineales son relativamente más fáciles y existen soluciones generales. Para las ecuaciones no lineales, en la mayoría de los casos, la solución general no existe y la solución puede ser un problema específico. Esto hace que la solución sea mucho más difícil que las ecuaciones lineales.


