Diferencia entre matriz y determinante

Matriz vs determinante
Las matrices y los determinantes son conceptos importantes es el álgebra lineal, donde las matrices proporcionan una forma concisa de representar grandes ecuaciones lineales y combinación, mientras que los determinantes están relacionados únicamente con un cierto tipo de matrices.
Más sobre matriz
Las matrices son matrices rectangulares de números donde los números están dispuestos en filas y columnas. El número de columnas y filas en una matriz determina el tamaño de la matriz. En general, una matriz está representada de manera idéntica por los soportes cuadrados, y los números están alineados en filas y columnas en el interior.

A se conoce como una matriz 3 × 3 porque tiene 3 columnas y 3 filas. Los números denotados por A_ij se llaman elementos e identificados de manera única por el número de fila y el número de columna. Además, la matriz se puede representar como [a_ij] _ (3 × 3), pero sus usos son limitados ya que los elementos no se dan explícitamente. Extendiendo el ejemplo anterior a un caso general podemos definir una matriz general de tamaño M × N;
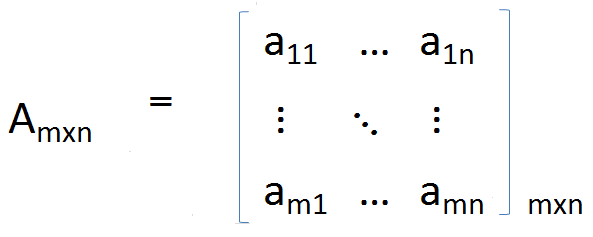
A tiene m filas y n columnas.
Las matrices se clasifican en función de sus propiedades especiales. Como ejemplo, una matriz con un número igual de filas y columnas se conoce como matriz cuadrada, y una matriz con una sola columna se conoce como vector.
Las operaciones en matrices se definen específicamente, pero sigan las reglas en álgebra abstracta. Por lo tanto, la adición, la resta y la multiplicación entre las matrices se realizan en un elemento en cuanto a. Para las matrices, la división no se define aunque existe lo inverso.
Las matrices son una representación concisa de una colección de números, y se puede usar fácilmente para resolver la ecuación lineal. Las matrices también tienen una amplia aplicación en el campo de álgebra lineal, con respecto a las transformaciones lineales.
Más sobre determinante
El determinante es un número único asociado con cada matriz cuadrada y se obtiene después de realizar un cierto cálculo para los elementos en la matriz. En la práctica, un determinante se denota colocando un signo de módulo para los elementos en la matriz. Por lo tanto, el determinante de A es dado por;
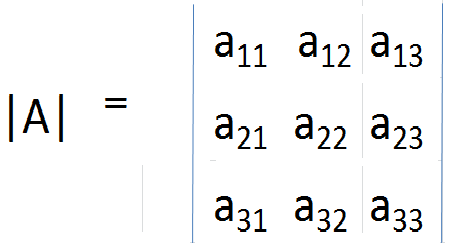
y generalmente para una matriz M × N
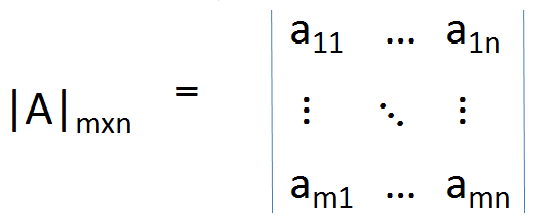
La operación para obtener el determinante es la siguiente;
| A | = ∑nortej = 1 aj CIJ, donde CIJ es el cofactor de la matriz dada por CIJ = (-1)i+j METROIJ.
El determinante es un factor importante que determina las propiedades de la matriz. Si el determinante es cero para una determinada matriz, el inverso de la matriz no existe.
¿Cuál es la diferencia entre matriz y determinante??
• Una matriz es un grupo de números, y un determinante es un número único relacionado con esa matriz.
• Se puede obtener un determinante de matrices cuadradas, pero no al revés. Un determinante no puede dar una matriz única asociada con ella.
• El álgebra sobre las matrices y los determinantes tiene similitudes y diferencias. Especialmente al realizar multiplicaciones. Por ejemplo, la multiplicación de matrices debe hacerse en cuanto al elemento, donde los determinantes son números individuales y siguen la multiplicación simple.
• Los determinantes se utilizan para calcular el inverso de la matriz y si el determinante es cero, el inverso de la matriz no existe.


