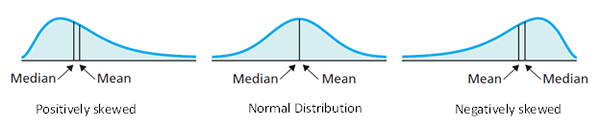
Diferencia entre media, mediana y modo

Media vs mediana vs modo
 

Media, mediana y modo son los principales medidas de tendencia central utilizado en estadísticas descriptivas. Son completamente diferentes entre sí y los casos en los que se utilizan para resumir los datos también son diferentes.

Significar

La media aritmética es la suma de los valores de datos divididos por el número de valores de datos, I.mi.

[latex] \ bar x = \ frac 1 n \ sum_ i = 1^n x_ i = \ frac x_ 1+x_ 2+x_ 3 +... +x_ n n [/latex] 

Si los datos son de un espacio de muestra, se llama media de muestra ([látex] \ bar x [/latex]), que es una estadística descriptiva de la muestra. Aunque es la medida descriptiva más utilizada para una muestra, no es una estadística robusta. Es muy sensible a los valores atípicos y oscilaciones.

Por ejemplo, considere el ingreso promedio de los ciudadanos de una ciudad en particular. Dado que todos los valores de datos se suman y luego se dividen, los ingresos de una persona extremadamente rica afecta la media significativamente. Por lo tanto, los valores medios no son una buena representación de los datos siempre.

Además, en el caso de una señal alterna, la corriente que pasa a través de un elemento varía periódicamente de la dirección positiva a la dirección negativa y viceversa. Si tomamos la corriente promedio que pasa por el elemento en un solo período, dará un 0, lo que significa que no ha pasado ninguna corriente a través del elemento, lo que obviamente no es cierto. Por lo tanto, en este caso también, la media aritmética no es una buena medida.

La media aritmética es un buen indicador cuando los datos se distribuyen uniformemente. Para una distribución normal, la media es igual al modo y mediana. También tiene los residuos más bajos cuando se considera el error cuadrado medio de raíz; Por lo tanto, la mejor medida descriptiva cuando se requiere representar un conjunto de datos por un solo número.

Mediana

Los valores del punto de datos medio después de organizar todos los valores de datos en orden ascendente se definen como la mediana del conjunto de datos. La mediana es el segundo cuartil, el quinto decil y el percentil 50.

• Si el número de observaciones (puntos de datos) es impar, entonces la mediana es la observación exactamente en el medio de la lista ordenada.

• Si el número de observaciones (puntos de datos) es uniforme, entonces la mediana es la media de las dos observaciones medias en la lista ordenada.

La mediana divide la observación en dos grupos; i.mi. un grupo (50%) de valores más altos y un grupo (50%) de valores más bajos que la mediana. Las medianas se usan específicamente en distribuciones sesgadas y representan datos bastante mejores que la media aritmética.

Modo

El modo es el número más ocurrido en un conjunto de observaciones. El modo de un conjunto de datos se calcula al encontrar la frecuencia de cada elemento dentro del conjunto.

• Si no se produce ningún valor más de una vez, el conjunto de datos no tiene modo.

• De lo contrario, cualquier valor que ocurra con la mayor frecuencia es un modo del conjunto de datos.

Puede existir más de 1 modo en un conjunto; Por lo tanto, el modo no es una estadística única de un conjunto de datos. En una distribución uniforme, hay un modo. El modo de una distribución de probabilidad discreta es el punto donde la función de masa de probabilidad alcanza su punto más alto. Renderizado de las interpretaciones anteriores, podemos decir que Maxima global son modos.

Considere la aplicación de las tres medidas al siguiente conjunto de datos.

Datos: 1, 1, 2, 3, 5, 5, 5, 5, 6, 6, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 14, 14, 15, 15 , 15

Media = (1+ 1+ 2+ 3+ 5+ 5+ 5+ 5+ 6+ 6+ 8+ 8+ 9+ 9+ 9+ 9+ 10+ 10+ 10+ 14+ 14+ 15+ 15+ 15 ) / 25 = 8.12

Mediana = 9 (13 ° elemento)

Modo = 9 (frecuencia de 9 = 5)

¿Cuál es la diferencia entre media, mediana y modo??

• La media aritmética es la suma de los valores (observaciones) divididas por el número de observaciones. No es una estadística robusta, y depende en gran medida de la naturaleza de distribución normal dentro de la distribución considerada. Un solo atípico puede causar un cambio significativo en la media que da valores relativamente engañosos. El concepto puede extenderse a la media geométrica, media armónica, media ponderada, etc.

• La mediana son los valores medios del conjunto de observaciones, y se ve relativamente menos afectado por los valores atípicos. Puede dar una buena estimación como la estadística resumida en casos altamente sesgados.

• El modo son los valores de observación más comunes en el conjunto de datos. Si la distribución es positiva sesgada, el modo se encuentra a la mediana y, si se sesga negativamente, el modo se encuentra directamente a la mediana.

• Si se sesga positivamente, la media es correcta a la mediana; Si la media sesgada negativamente es a la izquierda de la mediana.

• En la distribución normal, las tres, media, modo y mediana son iguales.