Diferencia entre la parábola y la hipérbola

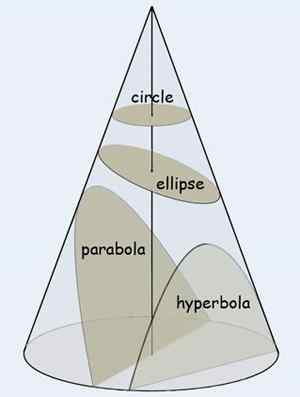
Parábola vs hipérbola

Kepler describió las órbitas de los planetas como elipses que luego fueron modificadas por Newton, ya que mostró que estas órbitas son secciones cónicas especiales como la parábola e hipérbola. Hay muchas similitudes entre una parábola y una hipérbola, pero también hay diferencias, ya que hay diferentes ecuaciones para resolver problemas geométricos que involucran estas secciones cónicas. Para comprender mejor las diferencias entre una parábola y una hipérbola, necesitamos comprender estas secciones cónicas.

Imagen cortesía: http: // cseligman.comunicarse

Una sección es una superficie o el contorno de esa superficie formada cortando una figura sólida con un plano. Si la cifra sólida es un cono, la curva resultante se llama sección cónica. El tipo y la forma de la sección cónica están determinadas por el ángulo de intersección del plano y el eje del cono. Cuando el cono se corta en ángulo recto con el eje, obtenemos una forma circular. Cuando se corta en menos de un ángulo recto, pero más que el ángulo realizado por el lado del cono da como resultado una elipse. Cuando se corta paralelo al lado del cono, la curva obtenida es una parábola y cuando se corta casi paralela al eje que al lado, obtenemos una curva conocida como hipérbola. Como puede ver en las figuras, los círculos y las elipses son curvas cerradas, mientras que las parábolas y las hipérbolas son curvas abiertas. En el caso de una parábola, los dos brazos finalmente se vuelven paralelos entre sí, mientras que en el caso de una hipérbola no es así.

Dado que los círculos y las parápolas se forman cortando un cono en ángulos específicos, todos los círculos tienen forma idéntica y todas las paracolas tienen forma idéntica. En el caso de Hyperbolas y elipses hay una amplia gama de ángulos entre el plano y el eje, por lo que tienden a tener una amplia gama de formas. Las ecuaciones de los cuatro tipos de secciones cónicas son las siguientes.

Círculo x²+Y²= 1

Elipse- x²/a²+ Y²/b²= 1

Parabola²= 4ax

Hiperbola- x²/a²- Y²/b²= 1