Diferencia entre paralelogramo y trapezoide

Paralelogramo vs trapezoide
Paralelograma y trapezoide (o trapecio) son dos cuadriláteros convexos. Aunque estos son cuadrángulos, la geometría del trapezoide difiere significativamente de los paralelogramas.
Paralelogramo
El paralelograma se puede definir como la figura geométrica con cuatro lados, con lados opuestos paralelos entre sí. Más precisamente es un cuadrilátero con dos pares de lados paralelos. Esta naturaleza paralela da muchas características geométricas a los paralelogramas.
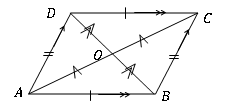
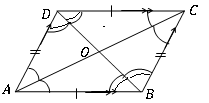
Un cuadrilátero es un paralelogramo si se encuentran las siguientes características geométricas.
• Dos pares de lados opuestos son de igual longitud. (AB = DC, AD = BC)
• Dos pares de ángulos opuestos son de igual tamaño. ([latex] d \ hat a b = b \ hat c d, a \ hat d c = a \ hat b c [/latex])
• Si los ángulos adyacentes son complementarios [látex] d \ hat a b + a \ hat d c = a \ hat d c + b \ hat c d = b \ hat c d + A \ hat b c = a \ hat b c + d \ hat a b = 180^\ circ = \ pi rad [/latex]
• Un par de lados, que se oponen entre sí, es paralelo y de igual longitud. (AB = DC y AB∥DC)
• Las diagonales se dividen entre sí (AO = OC, BO = OD)
• Cada diagonal divide el cuadrilátero en dos triángulos congruentes. (∆Adb ≡ ∆BCD, ∆ABC ≡ ∆Adc)
Además, la suma de los cuadrados de los lados es igual a la suma de los cuadrados de diagonales. Esto a veces se conoce como el ley de paralelograma y tiene aplicaciones generalizadas en física e ingeniería. (AB2 + antes de Cristo2 + CD2 + Cañón2 = AC2 + Bd2)
Cada una de las características anteriores se puede usar como propiedades, una vez que se establece que el cuadrilátero es un paralelogramo.
El área del paralelograma se puede calcular mediante el producto de la longitud de un lado y la altura al lado opuesto. Por lo tanto, el área del paralelograma se puede establecer como
Área de paralelograma = base × altura = Abundante×H
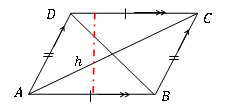
El área del paralelograma es independiente de la forma del paralelogramo individual. Depende solo de la longitud de la base y la altura perpendicular.
Si los lados de un paralelograma pueden ser representados por dos vectores, el área se puede obtener por la magnitud del producto vectorial (producto cruzado) de los dos vectores adyacentes.
Si los lados AB y AD están representados por los vectores ([látex] \ overrleinRarrow AB [/latex]) y ([látex] \ overrleinRightRarw ad [/latex]) respectivamente, el área del paralelogramo está dado por [ Látex] \ Izquierda | \ Overrightarrow AB \ Times \ OverrightRarrow AD \ Right | = AB \ CDOT AD \ sin \ alpha [/latex], donde α es el ángulo entre [látex] \ overrleinRarw ab [/latex] y [latex] \ overrleinRarrow ad [/latex].
Las siguientes son algunas propiedades avanzadas del paralelograma;
• El área de un paralelogramo es el doble del área de un triángulo creado por cualquiera de sus diagonales.
• El área del paralelograma se divide por la mitad por cualquier línea que pase a través del punto medio.
• Cualquier transformación afín no degenerada lleva un paralelogramo a otro paralelogramo
• Un paralelogramo tiene simetría rotacional del orden 2
• La suma de las distancias de cualquier punto interior de un paralelogramo a los lados es independiente de la ubicación del punto
Trapezoide
Trapecio (o Trapecio en inglés británico) es un cuadrilátero convexo donde al menos dos lados son paralelos y desiguales de longitud. Los lados paralelos del trapezoide se conocen como las bases y los otros dos lados se llaman las piernas.

Las siguientes son las principales características de los trapecios;
• Si los ángulos adyacentes no están en la misma base del trapecio, son ángulos complementarios. i.mi. Se suman a 180 ° ([látex] b \ hat a d+a \ hat d c = a \ hat b c+b \ hat c d = 180^\ circ [/ látex])
• Ambas diagonales de un trapecio se cruzan en la misma relación (la relación entre la sección de las diagonales es igual).
• Si A y B son bases y C, D son piernas, las longitudes de las diagonales están dadas por
[latex] \ sqrt \ frac ab^2 -a^2 b-ac^2+bd^2 b-a [/latex]
y
[latex] \ sqrt \ frac ab^2 -a^2 b-ac^2+bc^2 b-a [/latex]
El área del trapezoide se puede calcular utilizando la siguiente fórmula
Área de trapecio = [látex] \ frac a+b 2 \ times h [/latex]
¿Cuál es la diferencia entre paralelogramo y trapezoide (trapecio)?
• Tanto el paralelogramo como los trapezoides son cuadriláteros convexos.
• En un paralelogramo, ambos pares de los lados opuestos son paralelos mientras, en un trapezoide, solo un par es paralelo.
• Las diagonales del paralelograma se dividen entre sí (relación 1: 1) mientras que las diagonales del trapezoide se cruzan con una relación constante entre las secciones.
• El área del paralelograma depende de la altura y la base, mientras que el área del trapezoide depende de la altura y el segmento medio.
• Los dos triángulos formados por una diagonal en un paralelogramo siempre son congruentes, mientras que los triángulos del trapezoide pueden ser congruentes o no.


