Diferencia entre el grupo de puntos y el grupo espacial
Diferencia clave - Grupo de puntos vs Espacio Grupo
El grupo de puntos de los términos y el grupo espacial se utilizan en cristalografía. La cristalografía es el estudio de la disposición de los átomos en un sólido cristalino. El grupo de puntos cristalográficos es un conjunto de operaciones de simetría que dejan al menos un punto inmóvil. Una operación de simetría es un acto de obtener la imagen original de un objeto incluso después de moverlo. Las operaciones de simetría utilizadas en los grupos de puntos son rotaciones y reflexiones. Un grupo espacial es el grupo de simetría 3D de una configuración en el espacio. Un grupo de simetría es el grupo de todas las transformaciones obtenidas sin variar la composición durante la operación del grupo. El diferencia clave entre el grupo de puntos y el grupo espacial es que Hay 32 grupos de puntos cristalográficos, mientras que hay 230 grupos espaciales creados por la combinación de 32 grupos de puntos y 14 redes Bravais.
CONTENIDO
1. Descripción general y diferencia de claves
2. ¿Qué es el grupo de puntos?
3. ¿Qué es el grupo espacial?
4. Comparación de lado a lado - Grupo de puntos vs grupo espacial en forma tabular
5. Resumen
¿Qué es el grupo de puntos??
El grupo de puntos cristalográficos es un conjunto de operaciones de simetría que dejan al menos un punto inmóvil. Las operaciones de simetría descritas en los grupos de puntos son rotaciones y reflexiones. En las operaciones de simetría de grupo de puntos, un punto central en el objeto se mantiene sin mover (fijo) mientras se mueve otras caras del objeto a las posiciones de las características del mismo tipo. Allí, las características macroscópicas del objeto deben permanecer mismas antes y después de la operación de simetría.
Para cualquier objeto dado, hay un cierto número de operaciones de simetría posibles (con relaciones geométricas definidas entre operaciones de simetría). Se dice que el objeto tiene la simetría descrita por el grupo de puntos. Por lo tanto, los diferentes objetos que tienen diferentes simetrías de puntos son descritos por diferentes grupos de puntos.
En la notación de grupos de puntos, hay dos sistemas en uso;
-
Notación de las moscas
En el sistema de notación de Floenflies, los grupos de puntos se nombran como CNevada, CNueva Hampshire, DNueva Hampshire, Td, OH, etc. Los diferentes símbolos utilizados en este sistema de notación se dan a continuación.
- n es el mayor número de ejes de rotación
- V es el plano del espejo vertical (mencionado solo cuando no hay planos de espejo horizontal)
- H son los planos de espejo horizontal
- T es un grupo de puntos tetraédricos
- es un grupo de puntos octaédrico
Por ejemplo, Cnorte se usa indica que el grupo de puntos tiene el eje de rotación n-pliegue. Cuando se da como cNueva Hampshire, Significa que hay una Cnorte junto con un plano espejo (plano de reflexión) perpendicular al eje de rotación. En contraste, cNevada es cnorte con un plano espejo paralelo al eje de rotación. Si el grupo de puntos se da como S2n, Indica que el grupo de puntos tiene solo un eje de reflexión de rotación de 2n.
-
Notación de Hermann-Mauguin
El sistema de notación Hermann-Mauguin se usa comúnmente para grupos espaciales. Pero, también se usan para grupos de puntos cristalográficos. Da el eje de rotación más alto. Por ejemplo, el grupo de puntos que tiene solo 2 veces el eje de rotación se denota como 2. El grupo de puntos dado como c2h Por la notación de las moscas de la escuela se da como 2/m en el sistema de notación de Hermann-Mauguin en el que el símbolo 'M' indica un plano espejo y el símbolo de barra indica que el plano del espejo es perpendicular al eje doble. La siguiente tabla muestra diferentes anotaciones de grupos de puntos para diferentes sistemas de celosía.
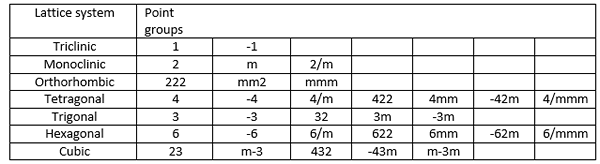

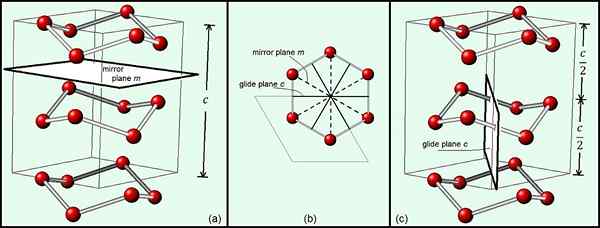
Figura 01: Los planos de espejo y los planos de deslizamiento de hielo hexagonal indican que el grupo espacial de hielo es P63/MMC
Hay 32 grupos de puntos. Los grupos de puntos más simples son 1, 2, 3, 4, 5 y 6. Todos estos grupos de puntos comprenden solo un eje de rotación. Para las inversiones rotativas, hay ejes llamados -1, m, -3, -4 y -6. Otros grupos de 22 puntos son combinaciones de estos grupos de puntos.
¿Qué es el grupo espacial??
Un grupo espacial es el grupo de simetría 3D de una configuración en el espacio. Hay 230 grupos espaciales. Estos 230 grupos son una combinación de 32 grupos de puntos cristalográficos (mencionados anteriormente) y 14 redes Bravais. El Redes de Bravais se dan en la tabla a continuación.
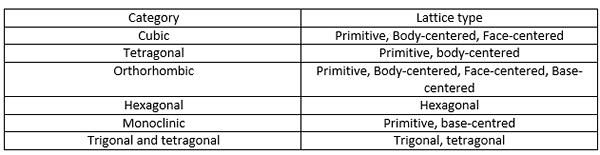
Un grupo espacial da una descripción de la simetría de un cristal. Los grupos espaciales son combinaciones de simetría de traducción de las operaciones de celda unitaria y simetría, como rotación, inversión rotativa, reflexión, eje de tornillo y operaciones de simetría de plano de deslizamiento.
¿Cuál es la diferencia entre el grupo de puntos y el grupo espacial??
Grupo de puntos vs grupo espacial | |
| El grupo de puntos cristalográficos es un conjunto de operaciones de simetría que dejan al menos un punto inmóvil. | Un grupo espacial es el grupo de simetría 3D de una configuración en el espacio. |
| Componentes | |
| Hay 32 grupos de puntos cristalográficos. | Hay 230 grupos espaciales (creados por la combinación de 32 grupos de puntos y 14 redes Bravais). |
| Operaciones de simetría | |
| Las operaciones de simetría utilizadas en la detección de grupos de puntos son la rotación y la reflexión. | Las operaciones de simetría utilizadas en la detección de grupos espaciales son la rotación, la inversión rotativa, la reflexión, el eje del tornillo y las operaciones de simetría del plano de deslizamiento. |
Resumen - Grupo de puntos vs Espacio Grupo
Los grupos de puntos y los grupos espaciales son términos descritos en cristalografía. El grupo de puntos cristalográficos es un conjunto de operaciones de simetría, todas las cuales dejan al menos un punto inmóvil. Un grupo espacial es el grupo de simetría 3D de una configuración en el espacio. La diferencia entre el grupo de puntos y el grupo espacial es que hay 32 grupos de puntos cristalográficos, mientras que hay 230 grupos espaciales (creados por la combinación de 32 grupos de puntos y 14 redes Bravais).
Referencia:
1."2: Operaciones de simetría y elementos de simetría."Bibliotecas de química, Librettexts, 6 de mayo de 2017. Disponible aquí
2."Grupo de puntos cristalográficos."Wikipedia, Fundación Wikimedia, 28 de febrero. 2018. Disponible aquí
Imagen de cortesía:
1.'Ice IH Space Group'by Dbuckingham42 - Trabajo propio, (CC By -Sa 4.0) a través de Commons Wikimedia