Diferencia entre postulado y teorema
Diferencia de clave: postulado vs teorema
Los postulados y los teoremas son dos términos comunes que a menudo se usan en matemáticas. Un postulado es una declaración que se supone que es verdadera, sin prueba. Un teorema es una declaración que puede demostrarse verdadera. Este es el diferencia clave entre el postulado y el teorema. Los teoremas a menudo se basan en postulados.
¿Qué es un postulado??
Un postulado es una declaración que se supone que es verdadera sin ninguna prueba. El Postulado es definido por el Diccionario de Oxford como "cosa sugerida o asumida como verdadera como la base para el razonamiento, la discusión o la creencia" y por el Diccionario del Patrimonio Americano como "algo asumido sin pruebas como ser evidente o generalmente aceptado, especialmente cuando se usa cuando se usa Como base para un argumento ".
Los postulados también se conocen como axiomas. Los postulados no tienen que ser probados ya que son visiblemente correctos. Por ejemplo, la declaración de que dos puntos hacen una línea es un postulado. Los postulados son la base de la cual se crean los teoremas y los lemas. Un teorema se puede derivar de uno o más postulados.
A continuación se muestran algunas características básicas que todos los postulados tienen:
- Los postulados deben ser fáciles de entender: no deben tener muchas palabras que sean difíciles de entender.
- Deben ser consistentes cuando se combinan con otros postulados.
- Deben tener la capacidad de ser utilizados de forma independiente.
Sin embargo, algunos postulados, como el postulado de Einstein de que el universo es homogéneo, no siempre son correctos. Un postulado puede volverse obviamente incorrecto después de un nuevo descubrimiento.

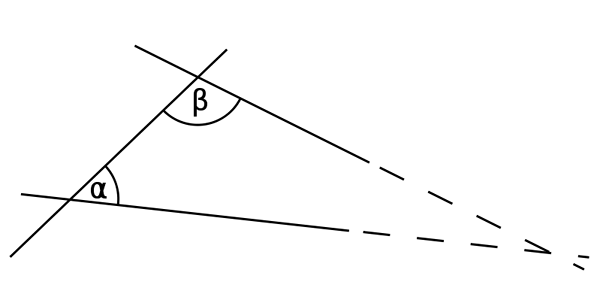
Si la suma de los ángulos interiores α y β es inferior a 180 °, las dos líneas rectas, producidas indefinidamente, se encuentran en ese lado.
Que es un teorema?
Un teorema es una declaración que puede probarse como verdadera. El Diccionario de Oxford define el teorema como una "proposición general no evidente, pero demostrada por una cadena de razonamiento; Una verdad establecida por medio de verdades aceptadas "y Merriam-Webster la define como" una fórmula, proposición o declaración en matemáticas o lógica deducida o deducida de otras fórmulas o proposiciones ".
Los teoremas se pueden probar mediante razonamiento lógico o mediante el uso de otros teoremas que ya han demostrado ser verdaderos. Un teorema que debe probarse para demostrar que otro teorema se llama lema. Tanto los lemas como los teoremas se basan en postulados. Un teorema generalmente tiene dos partes conocidas como hipótesis y conclusiones. Teorema de Pitágoras, el teorema de cuatro colores y el último teorema de Fermat son algunos ejemplos de teoremas.
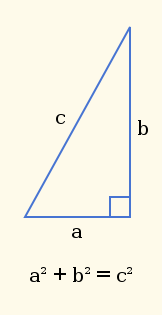
Visualización del teorema pitagórico
¿Cuál es la diferencia entre postulado y teorema??
Definición:
Postulado: El postulado se define como "una declaración aceptada como verdadera como la base del argumento o la inferencia."
Teorema: El teorema se define como "proposición general no evidente, pero es probada por una cadena de razonamiento; una verdad establecida por medio de verdades aceptadas ".
Prueba:
Postulado: Un postulado es una declaración que se supone que es verdadera sin ninguna prueba.
Teorema: Un teorema es una declaración que puede probarse como verdadera.
Relación:
Postulado: Los postulados son la base de los teoremas y los lemas.
Teorema: Los teoremas se basan en postulados.
Necesito probar:
Postulado: Los postulados no necesitan ser probados ya que dicen lo obvio.
Teorema: Los teoremas pueden probarse mediante razonamiento lógico o mediante el uso de otros teoremas que han demostrado ser verdaderos.
Imagen de cortesía:
"Teorema de Pitágoras ABC" de Pitágoras ABC.PNG: NL: Gebruiker: Andre_engels - Pythágoras ABC.PNG (CC BY-SA 3.0) a través de Commons Wikimedia
"Postulado paralelo en" por 6054 - Editar de http: // PL.Wikipedia.org/wiki/grafika: paralelo_postulado.SVG por usuario: Harkonnen2 (CC BY-SA 3.0) a través de Commons Wikimedia


