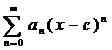Diferencia entre la serie de potencia y la serie Taylor

Serie Power Vs Taylor
En matemáticas, una secuencia real es una lista ordenada de números reales. Formalmente, es una función desde el conjunto de números naturales en el conjunto de números reales. Si anortees entoncesth término de una secuencia, denotamos la secuencia por o por a1, a2,… ,anorte,… .Por ejemplo, considere la secuencia 1, ½, ⅓, .. , 1/norte,… . Se puede denotar como 1/n.
Es posible definir una serie usando secuencias. Una serie es la suma de los términos de una secuencia. Por lo tanto, para cada secuencia, hay una secuencia asociada y viceversa. Si anorte es la secuencia bajo consideración, entonces, la serie formada por esa secuencia puede representarse como:
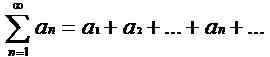
Por lo tanto, en el ejemplo anterior, la serie asociada es 1+1/2+1/3+… + 1/norte +… .
Como sugieren los nombres, la serie Power es un tipo especial de serie y se usa ampliamente en análisis numérico y modelado matemático relacionado. La serie Taylor es una serie de potencia especial que proporciona una forma alternativa y fácil de manipular de representar funciones bien conocidas.
¿Qué es la serie Power?
Una serie de potencia es una serie de la forma
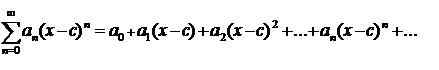
que es convergente (posiblemente) para algún intervalo centrado en C. Los coeficientes anorte puede ser números reales o complejos, y es independiente de X; i.mi. la variable ficticia.
Por ejemplo, configurando anorte= 1 para cada norte, y C = 0, la serie de potencia 1+x+x2+… + Xnorte+… es obtenido. Es fácil observar que cuando x ε (-1,1), esta serie de potencia converge a 1/(1-x).
Una serie de potencia converge cuando X = C. Los otros valores de X para el cual la serie de energía converge siempre tomará la forma de un intervalo abierto centrado en C. Eso es, Habrá un valor 0≤ R ≤ ∞ tal que para cada X satisfactorio | X-C | ≤Riñonal, la serie de potencia es convergente y para cada X satisfactorio | X-C |>Riñonal, La serie Power es divergente. Este valor Riñonal se llama radio de convergencia de la serie de potencia (Riñonal puede tomar cualquier valor real o infinito positivo).
La serie de potencia se puede agregar, restar, multiplicarse y dividirse utilizando las siguientes reglas. Considere las dos series de potencia:
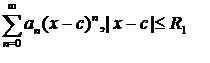
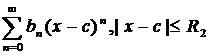 .
.
Entonces,
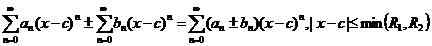
i.mi. Los términos similares se agregan o se restan juntos. Además, es posible multiplicar y dividir las dos series de potencia utilizando la identidad,
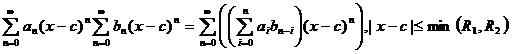
¿Qué es la serie Taylor??
La serie Taylor se define para una función F(X) que es infinitamente diferenciable en un intervalo. Asumir F(X) es diferenciable en un intervalo centrado en C. Entonces la serie de potencia que está dada por
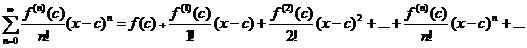
se llama expansión de la serie Taylor de la función F(X) acerca de C. (Aquí F(norte)(C) Denota el nth derivado en X = C). En el análisis numérico, se usa un número finito de términos en esta expansión infinita para calcular los valores en los puntos donde la serie es convergente a la función original.
Una función F(X) se dice que es analítico en el intervalo (A, B), si para cada x ε (a, b), la serie Taylor de F(X) converge a la función F(X). Por ejemplo, 1/(1-x) es analítico en (-1,1), ya que su expansión de Taylor 1+x+x2+… + Xnorte+... converge a la función en ese intervalo, y miX es analítico en todas partes, desde la serie Taylor de miXconverge a miX Para cada número real X.
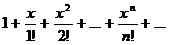
¿Cuál es la diferencia entre la serie de potencia y la serie Taylor??
1. La serie Taylor es una clase especial de series de potencia definida solo para funciones que son infinitamente diferenciables en algún intervalo abierto.
2. Serie Taylor Tome el formulario especial
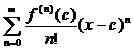
Mientras que una serie de potencia puede ser cualquier serie de la forma