Diferencia entre rectángulo y rombo

Rectángulo vs rombo
Rombo y rectángulo son cuadriláteros. La geometría de estas cifras era conocida por el hombre durante miles de años. El tema es tratado explícitamente en el libro "Elementos" escrito por el matemático griego Euclid.
Paralelogramo
El paralelograma se puede definir como la figura geométrica con cuatro lados, con lados opuestos paralelos entre sí. Más precisamente es un cuadrilátero con dos pares de lados paralelos. Esta naturaleza paralela da muchas características geométricas a los paralelogramas.
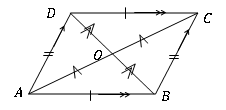
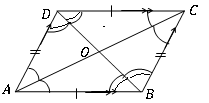
Un cuadrilátero es un paralelogramo si se encuentran las siguientes características geométricas.
• Dos pares de lados opuestos son de igual longitud. (AB = DC, AD = BC)
• Dos pares de ángulos opuestos son de igual tamaño. ([latex] d \ hat a b = b \ hat c d, a \ hat d c = a \ hat b c [/latex])
• Si los ángulos adyacentes son complementarios [látex] d \ hat a b + a \ hat d c = a \ hat d c + b \ hat c d = b \ hat c d + A \ hat b c = a \ hat b c + d \ hat a b = 180^\ circ = \ pi rad [/latex]
• Un par de lados, que se oponen entre sí, es paralelo y de igual longitud. (AB = DC y AB∥DC)
• Las diagonales se dividen entre sí (AO = OC, BO = OD)
• Cada diagonal divide el cuadrilátero en dos triángulos congruentes. (∆Adb ≡ ∆BCD, ∆ABC ≡ ∆Adc)
Además, la suma de los cuadrados de los lados es igual a la suma de los cuadrados de diagonales. Esto a veces se conoce como el ley de paralelograma y tiene aplicaciones generalizadas en física e ingeniería. (AB2 + antes de Cristo2 + CD2 + Cañón2 = AC2 + Bd2)
Cada una de las características anteriores se puede usar como propiedades, una vez que se establece que el cuadrilátero es un paralelogramo.
El área del paralelograma se puede calcular mediante el producto de la longitud de un lado y la altura al lado opuesto. Por lo tanto, el área del paralelograma se puede establecer como
Área de paralelograma = base × altura = Abundante×H
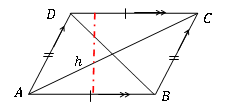
El área del paralelograma es independiente de la forma del paralelogramo individual. Depende solo de la longitud de la base y la altura perpendicular.
Si los lados de un paralelograma pueden ser representados por dos vectores, el área se puede obtener por la magnitud del producto vectorial (producto cruzado) de los dos vectores adyacentes.
Si los lados AB y AD están representados por los vectores ([látex] \ overrleinRarrow AB [/latex]) y ([látex] \ overrleinRightRarw ad [/latex]) respectivamente, el área del paralelogramo está dado por [ Látex] \ Izquierda | \ Overrightarrow AB \ Times \ OverrightRarrow AD \ Right | = AB \ CDOT AD \ sin \ alpha [/latex], donde α es el ángulo entre [látex] \ overrleinRarw ab [/latex] y [latex] \ overrleinRarrow ad [/latex].
Las siguientes son algunas propiedades avanzadas del paralelograma;
• El área de un paralelogramo es el doble del área de un triángulo creado por cualquiera de sus diagonales.
• El área del paralelograma se divide por la mitad por cualquier línea que pase a través del punto medio.
• Cualquier transformación afín no degenerada lleva un paralelogramo a otro paralelogramo
• Un paralelogramo tiene simetría rotacional del orden 2
• La suma de las distancias de cualquier punto interior de un paralelogramo a los lados es independiente de la ubicación del punto
Rectángulo
Un cuadrilátero con cuatro ángulos rectos se conoce como rectángulo. Es un caso especial del paralelogramo donde los ángulos entre dos lados adyacentes son ángulos rectos.
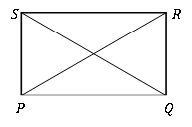
Además de todas las propiedades de un paralelograma, se pueden reconocer características adicionales al considerar la geometría del rectángulo.
• Cada ángulo en los vértices es un ángulo recto.
• Las diagonales son de igual longitud, y se dividen entre sí. Por lo tanto, las secciones bisectadas también tienen la misma longitud.
• La longitud de las diagonales se puede calcular utilizando el teorema de Pitágoras:
Pq2 + PD2 = SQ2
• La fórmula del área se reduce al producto de la longitud y el ancho.
Área de rectángulo = longitud × ancho
• Muchas propiedades simétricas se encuentran en un rectángulo, como;
- Un rectángulo es cíclico, donde se pueden colocar todos los vértices en el perímetro de un círculo.
- Es equiangular, donde todos los ángulos son iguales.
- Es isogonal, donde todas las esquinas se encuentran dentro de la misma órbita de simetría.
- Tiene simetría reflexional y simetría rotacional.
Rombo
Un cuadrilátero con todos los lados es de igual longitud se conoce como rombo. También se nombra como un cuadrilátero equilibrado. Se considera que tiene una forma de diamante, similar a la de las cartas de juego.
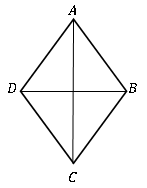
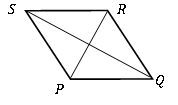
El rombo también es un caso especial del paralelogramo. Se puede considerar como un paralelogramo con los cuatro lados iguales. Y tiene siguiendo propiedades especiales, además de las propiedades de un paralelogramo.
• Las diagonales del rombo se dividen entre sí en ángulo recto; Las diagonales son perpendiculares.
• Las diagonales dividen los dos ángulos internos opuestos.
• Al menos dos de los lados adyacentes son de igual longitud.
El área del rombo se puede calcular en el mismo método que el paralelogramo.
¿Cuál es la diferencia entre rombo y rectángulo??
• El rombo y el rectángulo son cuadriláteros. Rectángulo y rombo son casos especiales de los paralelogramas.
• El área de cualquiera se puede calcular utilizando la fórmula base × altura.
• Teniendo en cuenta las diagonales;
- Las diagonales del rombo se dividen entre sí en ángulo recto, y los triángulos formados son equilibrados.
- Las diagonales del rectángulo tienen la misma longitud y se bisigen entre sí; Las secciones bisectadas tienen la misma longitud. Las diagonales dividen el rectángulo en dos triángulos rectos congruentes.
• Considerando los ángulos internos;
- Los ángulos internos del rombo son bisectados por las diagonales
- Los cuatro ángulos internos del rectángulo son ángulos rectos.
• considerando los lados;
- Como los cuatro lados son iguales en un rombo, cuatro veces el cuadrado de un lado es igual a la suma de los cuadrados de la diagonal (usando la ley de paralelogramo)
- En los rectángulos, la suma de los cuadrados de los dos lados adyacentes es igual al cuadrado de la diagonal en los extremos. (Regla de Pitágoras)


