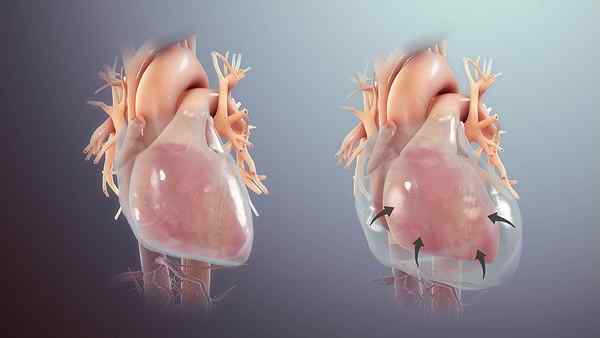
Diferencia entre relación y función

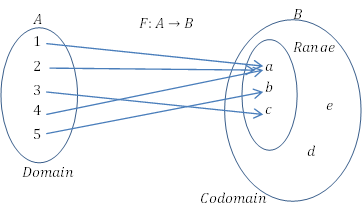
Relación vs función
 

Desde las matemáticas de la escuela secundaria en adelante, la función se convierte en un término común. Aunque se usa con bastante frecuencia, se usa sin una comprensión adecuada de su definición e interpretaciones. Este artículo se centra en describir esos aspectos de una función.

Relación

Una relación es un vínculo entre los elementos de dos conjuntos. En un entorno más formal, se puede describir como un subconjunto del producto cartesiano de dos conjuntos X e Y. El producto cartesiano de x e y, denotado como x × y, es un conjunto de pares ordenados que consisten en elementos de los dos conjuntos, a menudo denotados como (x, y). Los conjuntos no tienen que ser diferentes. Por ejemplo, un subconjunto de elementos de un × A, se llama relación en un.

Función

Las funciones son un tipo especial de relaciones. Este tipo especial de relación describe cómo se asigna un elemento a otro elemento en otro conjunto o en el mismo conjunto. Para que la relación sea una función, se deben satisfacer dos requisitos específicos.

Cada elemento del conjunto donde se inicia cada mapeo debe tener un elemento asociado/vinculado en el otro conjunto.

Los elementos en el conjunto donde comienza el mapeo solo se pueden asociar/vincular a uno y solo un elemento en el otro conjunto

El conjunto del que se mapea la relación se conoce como el dominio. El conjunto, donde se asigna la relación se conoce como codominio. El subconjunto de elementos en el codominio que contiene solo los elementos vinculados a la relación se conoce como el rango.

Técnicamente, una función es una relación entre dos conjuntos, donde cada elemento en un conjunto se asigna de forma única a un elemento en el otro.

 Observe lo siguiente

• Cada elemento en el dominio se asigna al codominio.
• Varios elementos del dominio están conectados con el mismo valor en el codominio, pero un solo elemento del dominio no se puede conectar a más de un elemento del codomain. (El mapeo tiene que ser único)
• Si cada elemento del dominio se asigna a elementos distintos y únicos en el codominio, se dice que la función es una función "individual".

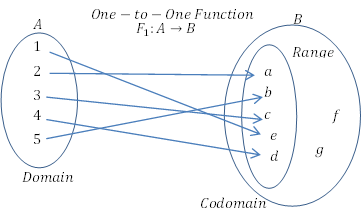
• El codominio contiene elementos que no sean los que se conectan a los elementos del dominio. La gama no tiene que ser el codominio. Si el codominio es igual al rango, la función se conoce como una función "sobre".

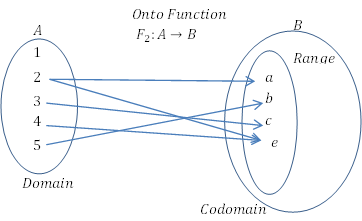
Cuando los valores que pueden tomar la función son reales, se denomina función real. Los elementos de codomain y dominio son números reales.

Las funciones siempre se denotan usando variables. Los elementos del codomain están representados simbólicamente por la variable. La notación f (x) representa los elementos del rango. La relación se puede representar usando la expresión en la forma f (x) = x^2. Dice que el elemento del dominio se mapea en el cuadrado del elemento, dentro del codomain. 

¿Cuál es la diferencia entre la función y la relación??

• Las funciones son un tipo especial de relaciones.

• La relación se basa en el producto cartesiano de dos conjuntos.

• La función se basa en relaciones con propiedades específicas.

• El dominio de una función debe asignarse en el codominio de modo que cada elemento tenga un valor correspondiente y determinado de forma única en el codomain. La relación puede vincular un elemento único a múltiples valores.