Diferencia entre la transposición y la matriz inversa

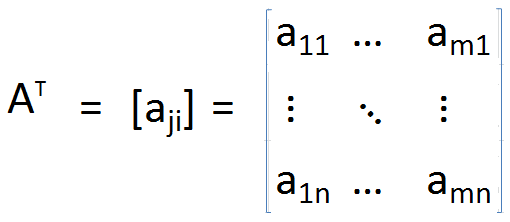
Transposición vs matriz inversa
 

La transposición y la inversa son dos tipos de matrices con propiedades especiales que encontramos en la álgebra matricial. Son diferentes entre sí y no comparten una relación cercana, ya que las operaciones realizadas para obtenerlas son diferentes.

Tienen amplias aplicaciones en el campo de álgebra lineal y las implementaciones derivadas como la informática.

Más sobre la matriz de transposición

Transposición de una matriz A se puede identificar como la matriz obtenida al reorganizar las columnas como filas o filas como columnas. Como resultado, los índices de cada elemento se intercambian. Más formalmente, Transpose de matriz A, Se define como

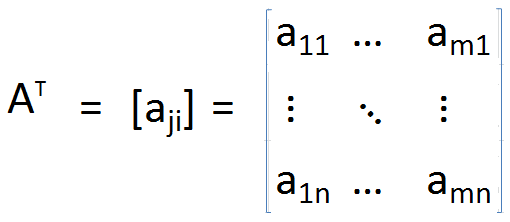
dónde

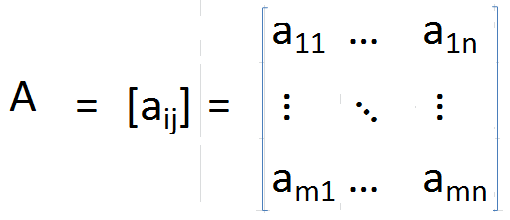
En una matriz de transposición, la diagonal permanece sin cambios, pero todos los demás elementos se giran alrededor de la diagonal. Además, el tamaño de las matrices también cambia de M × N a N × M.

La transposición tiene algunas propiedades importantes, y permiten una manipulación más fácil de matrices. Además, algunas matrices de transposición importantes se definen en función de sus características. Si la matriz es igual a su transposición, entonces la matriz es simétrica. Si la matriz es igual a su negativo de la transposición, la matriz es un sesgo simétrico. La transposición conjugada de una matriz es la transposición de la matriz con los elementos reemplazados por su complejo conjugado.

Más sobre la matriz inversa

El inverso de una matriz se define como una matriz que da la matriz de identidad cuando se multiplica juntos. Por lo tanto, por definición, si AB = BA = I entonces B es la matriz inversa de A y A es la matriz inversa de B. Entonces, si consideramos B = A^-1 , entonces Automóvil club británico^-1 = A^-1A = i

Para que una matriz sea invertible, la condición necesaria y suficiente es que el determinante de A no es cero; i.E |A| = det (A) ≠ 0. Se dice que una matriz es invertible, no síntecular o no degenerativa si satisface esta condición. Resulta que A es una matriz cuadrada y ambos A^-1 y A tiene el mismo tamaño.

El inverso de la matriz A Se puede calcular por muchos métodos en álgebra lineal, como la eliminación gaussiana, la composición de proposición a la propagación, la descomposición de Cholesky y la regla de Carmer. Una matriz también se puede invertir mediante el método de inversión de bloques y la serie Neuman.

¿Cuál es la diferencia entre la matriz de transposición y inversa??

• La transposición se obtiene reorganizando las columnas y las filas en la matriz, mientras que el inverso se obtiene mediante un cálculo numérico relativamente difícil. (Pero en realidad ambos son transformaciones lineales)

• Como resultado directo, los elementos en la transposición solo cambian su posición, pero los valores son los mismos. Pero en el inverso, los números pueden ser completamente diferentes de la matriz original.

• Cada matriz puede tener una transposición, pero el inverso se define solo para matrices cuadradas, y el determinante debe ser un determinante distinto de cero.